1.合并两个数组（简单）

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
         int p1 = m - 1, p2 = n - 1;// 指向两个数组的最后一个元素
         int p = m + n - 1;// 指向合并后数组的最后一个元素
        // 从后往前比较，将较大的元素放入合并后的数组中
         while (p1 >= 0 && p2 >= 0) {
             nums1[p--] = nums1[p1] > nums2[p2] ? nums1[p1--] : nums2[p2--];
         }
        //如果num1的数全部遍历完毕了，但len2还没有遍历，所以只要将len2剩余的元素全部复制到len1中，此时len2的长度根据len2中剩下的元素的长度来决定
        //但是如果num2全部遍历完了，那么此时的len2就是为-1了，所以当你在将num2复制到num1时，复制的长度为0，所以不复制任何元素过去
         System.arraycopy(nums2, 0, nums1, 0, p2 + 1);
    }

}

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
   // 指向两个数组的最后一个元素
        int p1 = m-1;
        int p2 = n-1;
        int p = m+n-1;// 指向合并后数组的最后一个元素
   // 从后往前比较，将较大的元素放入合并后的数组中
        while(p2>=0){
  // 如果 nums1 还有剩余元素，且当前 nums1 的元素大于等于 nums2 的元素
            if(p1>=0&&nums1[p1]>nums2[p2]){
               // 将 nums1 的元素放入合并后的数组中，并向前移动指针
                nums1[p--]=nums1[p1--];
            }
            else{
                //将nums2的元素放入合并后的数组，并向前移动指针
 // 注意这里不需要判断 p2 是否大于等于 0，因为当 nums1 没有剩余元素时，p1 也已经小于 0 了
                nums1[p--]= nums2[p2--];
            }
        }
    }
}
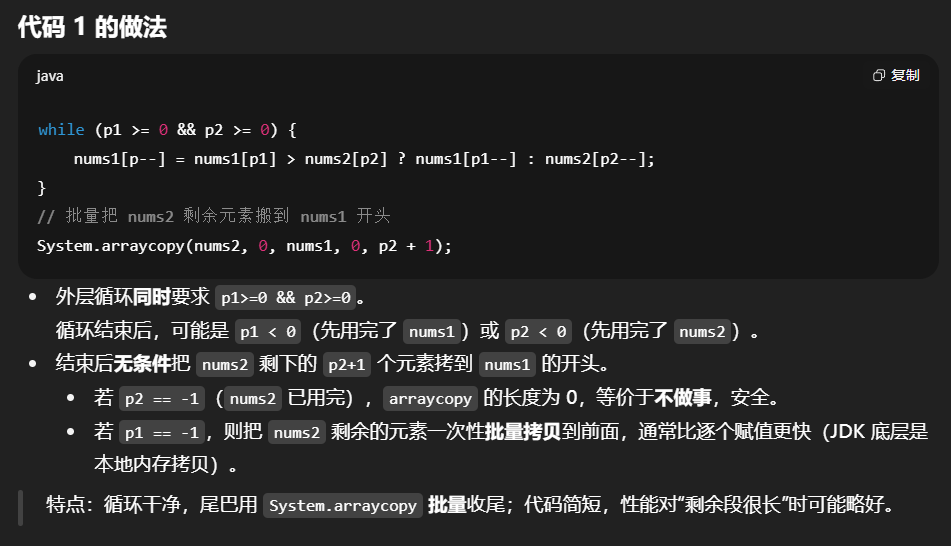
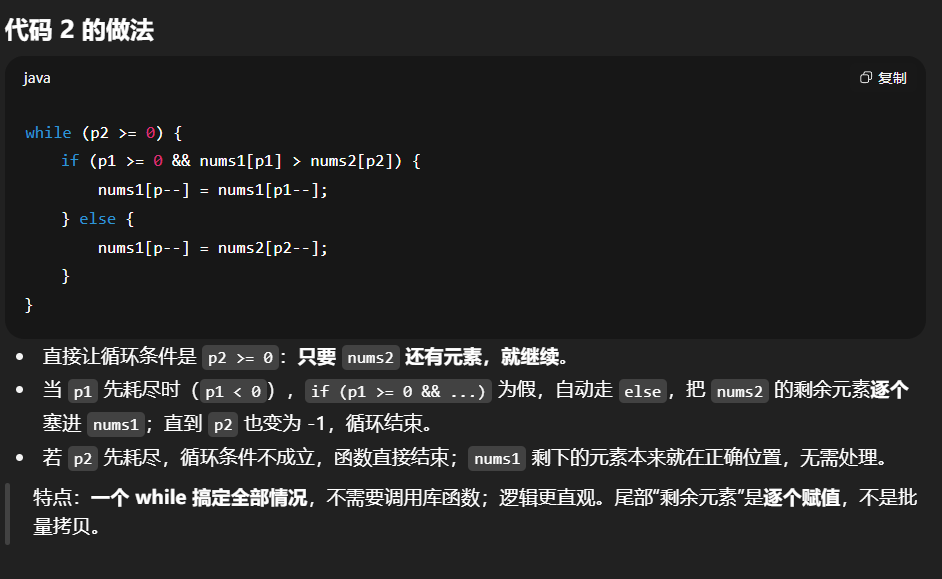
  • 三个指针：p1=m-1 指向 nums1 有效区末尾，p2=n-1 指向 nums2 末尾，p=m+n-1 指向合并后数组末尾。
  • 每次比较 nums1[p1] 和 nums2[p2]，把较大的放到 nums1[p]，指针左移。
  • 相等时两段代码都把 nums2[p2] 放进去（因为用的是 > 而不是 >=）。

img

img

2.移除元素（简单）

img

img

本题只需要返回k（不包含val的元素个数）

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int removeElement(int[] nums, int val) {
        if(nums.length == 0) return 0;
        int i = 0;
        //遍历数组，如果当前元素不等于val，则将其放到前面去
        for(int j = 0;j < nums.length;j++){
            if(nums[j] != val){
                nums[i++] = nums[j];
            }
        }
        return i;
    }
}

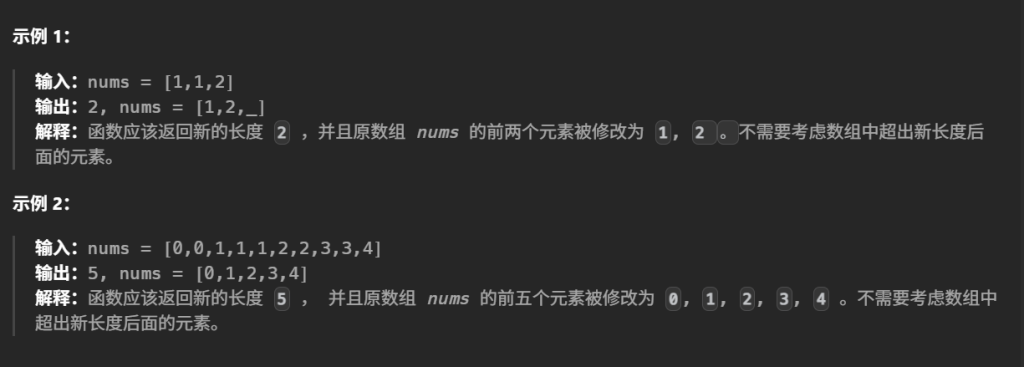
3.删除有序数组中的重复项（简单）

img

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int removeDuplicates(int[] nums) {
       if(nums.length == 0) return 0;
       int i = 0;//指向下一个不重复的元素的位置
        //遍历数组，如果当前元素不等于前一个元素，则将其放到前面去
       for(int j = 1;j < nums.length;j++){
           if(nums[i] != nums[j]){
               i++;
               nums[i] = nums[j];//将不重复的元素放到前面去
           }
           
       }
       return i+1;
    }
}

  • i 表示数组去重后的最后一个元素下标。

  • 因为数组下标是从 0 开始的，所以 数组的长度应该是下标 + 1。

  • 比如输入

    1
    [1,1,2]

    ：

    • 最终数组变成 [1,2,...]；
    • i = 1，但是长度是 2 → 所以返回 i+1。

👉 这里的返回值是 长度，所以必须 i+1。

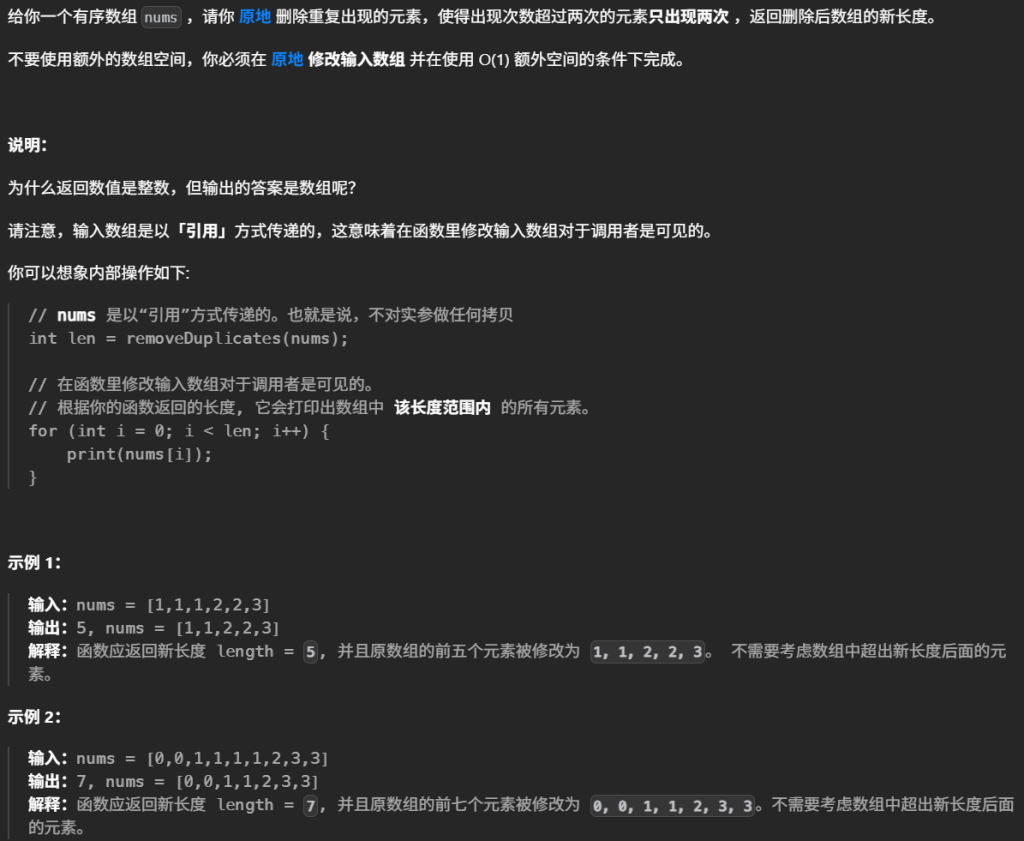
4.删除有序数组中的重复项II（中等）

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int removeDuplicates(int[] nums) {
        int n = nums.length;
       if(n <= 2) return nums.length;
       int i =2;//指向下一个不重复的元素的位置
        //遍历数组，如果当前元素不等于前一个元素，则将其放到前面去
        for (int j = i; j < n; j++) {
            if(nums[j] != nums[i-2]){
                nums[i] = nums[j];
                i++;
                
            }
        }
        return i;
    }
}

i 表示数组去重后下一个应该放置新元素的位置。

当循环结束时，i 已经 指向去重数组末尾的下一个位置。

因为 i 本身就是新数组的长度，所以直接返回 i。

比如输入 [1,1,1,2,2,3]：

  • 处理完后数组变为 [1,1,2,2,3,...]；
  • i = 5，去重后的长度就是 5，直接返回 i。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int removeDuplicates(int[] nums) {
        int n = nums.length, l = 2, r = 2;

        while (r < n) {
            if (nums[r] != nums[l - 2]) {
                nums[l] = nums[r];
                l++;
            }

            r++;
        }

        return l;
    }
}

5.最后一个单词的长度(简单)

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
 class Solution {
    public int lengthOfLastWord(String s) {
           if(s.length()==0) return 0;
           //去掉字符串末尾的空格
           String[] strs = s.split(" ");
           int n = strs.length-1;//最后一个单词的下标
          //从后往前遍历，找到最后一个单词的长度
           for(int i=n;i>=0;i--){
               //当遇到非空字符串时，返回长度
               if(!strs[i].equals("")){
                   return strs[i].length();
               }
           }
           return 0;
    }
}

📌 例子 1

输入：

1
s = "   fly me   to   the moon  "
  1. split 之后
1
String[] strs = s.split(" ");

因为 " " 作为分隔符，连续空格会被切成很多 ""，结果数组是：

1
["", "", "", "fly", "me", "", "", "to", "", "", "the", "moon", "", ""]
  1. 从后往前遍历
  • i = 13 → strs[13] = "" → 空字符串，跳过
  • i = 12 → strs[12] = "" → 空字符串，跳过
  • i = 11 → strs[11] = "moon" → 非空字符串！说明我们找到了最后一个单词
    👉 直接返回 "moon".length() = 4

所以输出是 4。

📌 为什么不是“遇到空字符串就说明最后一个单词结束”？

这里要注意：

  • split(" ") 会产生很多空字符串 ""，但这些并不是“单词结束”的标志，而只是因为多个空格被切出来的无效元素。
  • 真正的 单词 一定是 非空字符串。
  • 因此要找“最后一个单词”，就要从后往前，遇到第一个 非空字符串 才返回长度。

📌 再看例子 2

输入：

1
s = "Hello World"

split 后：

1
["Hello", "World"]

从后往前遍历：

  • i=1 → "World"，非空，直接返回 5。

✅ 总结：
你的理解差了一点点：

  • 空字符串 "" 只是空格切出来的垃圾，不代表单词结束。
  • 第一个非空字符串才是最后一个单词。

6.最长公共前缀（简单）

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public String longestCommonPrefix(String[] strs) {
         if(strs.length==0) return "";
         String prefix = strs[0];//初始化最长公共前缀为第一个字符串
        //遍历字符串数组，逐个与当前最长公共前缀进行比较
         for(int i = 1; i < strs.length; i++){
             //如果当前字符串不是以最长公共前缀开头，则更新最长公共前缀
             while(strs[i].indexOf(prefix) != 0){
                 //去掉最长公共前缀的最后一个字符，直到当前字符串以更新后的最长公共前缀开头或最长公共前缀为空
                 prefix = prefix.substring(0, prefix.length() - 1);
                 if(prefix.isEmpty()) return "";
             }
         }
         return prefix;
    }
}

核心思路

  1. 假设第一个字符串是最长公共前缀 prefix。

  2. 从第二个字符串开始，逐个和 prefix 对比。

  3. 如果当前字符串不是以

    1
    prefix

    开头，就不断缩短

    1
    prefix

    （去掉末尾字符），直到：

    • 当前字符串以 prefix 开头，或者
    • prefix 为空（说明不存在公共前缀）。

  4. 最终返回 prefix。

好的，我们一步步讲解这个 最长公共前缀 (Longest Common Prefix) 的代码逻辑。

🔎 流程拆解（以示例 ["flower", "flow", "flight"] 为例）

初始化

1
String prefix = strs[0]; // "flower"

假设公共前缀就是第一个字符串 "flower"。

第 1 轮对比：和 “flow” 比

检查 "flow".indexOf("flower")：

  • 返回 -1，说明 "flow" 不是以 "flower" 开头。
    于是进入 while 循环，逐步缩短 prefix：
  • "flow".indexOf("flowe") → -1
  • "flow".indexOf("flow") → 0 ✅

此时 prefix = "flow"。

第 2 轮对比：和 “flight” 比

检查 "flight".indexOf("flow")：

  • 返回 -1，不是以

    1
    "flow"

    开头。缩短：

    • "flight".indexOf("flo") → -1
    • "flight".indexOf("fl") → 0 ✅

此时 prefix = "fl"。

结束

所有字符串对比完毕，prefix = "fl"，返回结果 "fl"。

📌 示例 2：["dog","racecar","car"]

  • 初始化 prefix = "dog"

  • 比较

    1
    "racecar"

    ：

    1
    "racecar".indexOf("dog") = -1

    → 缩短 prefix：

    • "do" → -1
    • "d" → -1
    • "" → 空，直接返回 ""。

所以结果是 ""。

✅ 总结

这个代码的特点：

  • 逐步收缩法：每次缩短 prefix，直到满足条件。
  • 利用 indexOf：判断字符串是否以 prefix 开头。
  • 最坏情况：所有字符串完全相同 → 遍历一次即可；所有字符串完全不同 → 最快返回 ""。

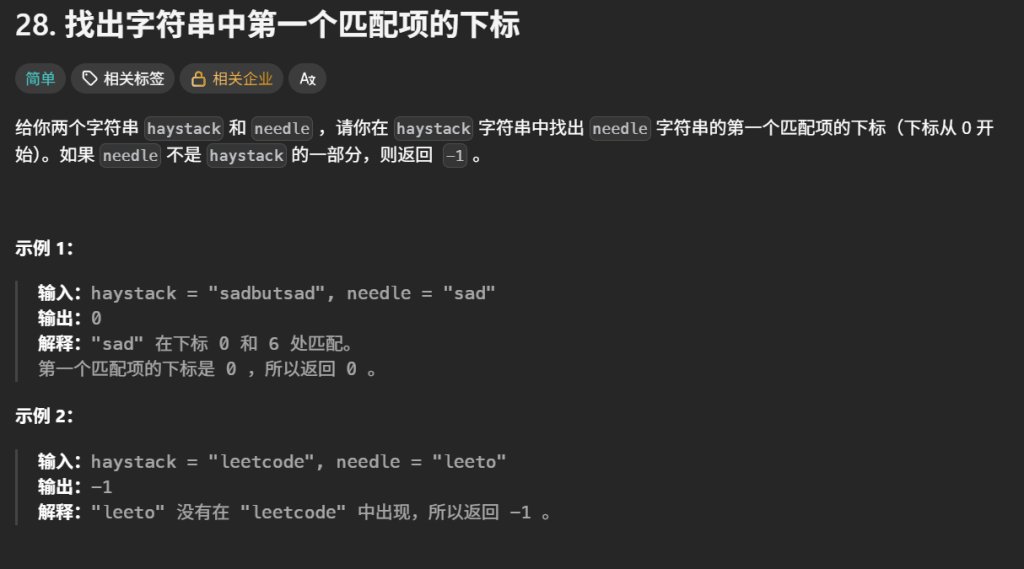
7.找出字符串中第一个匹配项的下标（简单）

img

1
2
3
4
5
6
7
class Solution {
    public int strStr(String haystack, String needle) {
        //if(needle.isEmpty()) return 0;
        //if(haystack.isEmpty()) return -1;
        return haystack.indexOf(needle);
    }
}

一行搞定

用一行 haystack.indexOf(needle) 就能解决「找子串第一次出现的位置」的问题，确实比我们自己写双重循环、KMP 算法看起来简单很多。原因在于 indexOf 已经帮我们封装好了整个查找过程。我来详细讲讲它的原理。

  1. indexOf 的作用

在 Java 中：

1
int index = haystack.indexOf(needle);

返回 子串 needle 在 haystack 中第一次出现的下标。

  • 如果存在 → 返回第一个匹配的下标。
  • 如果不存在 → 返回 -1。

这正好就是 LeetCode 第 28 题要求的功能。

  1. indexOf 的原理

不同 JDK 版本底层实现略有差别，但思路大致一样。核心是 字符串匹配算法：

常见的实现方式

  1. 暴力匹配（Brute Force）
    • 遍历 haystack 的每个可能起点 i，
    • 检查从 i 开始的子串是否等于 needle。
    • 时间复杂度：O(n * m)，其中 n = haystack 长度，m = needle 长度。
      （在 needle 很短的场景下，这种方法足够快。）
  2. Boyer-Moore / KMP 等优化算法
    • 为了减少回溯，indexOf 在一些 JDK 中会用到 Boyer-Moore 的 “坏字符规则” 优化。
    • 这样平均复杂度接近 O(n)。
  3. 本地优化（Native Code / Intrinsics）
    • 在一些 JVM 实现中，如果 needle 只有一个字符，直接调用更快的 char[] 扫描函数（比如 C 的 memchr）。
    • 如果 needle 较长，可能结合多种策略。
  1. 为什么一行就能做？

因为 indexOf 本身就是一个完整的子串查找实现，它在 JDK 里已经帮我们写好了底层逻辑，并且做了大量优化：

  • 边界情况（空字符串、needle 长度大于 haystack 等）。
  • 不同场景下选择最优算法。
  • 对底层 char[] 做了高效比较。

所以，我们直接调用 indexOf，等价于自己写完整的查找过程。

  1. 举个例子走一遍
1
2
haystack = "sadbutsad";
needle   = "sad";
  • indexOf 从位置 0 开始比对：
    haystack[0…2] = “sad”，刚好等于 needle → 返回 0。

再比如：

1
2
haystack = "leetcode";
needle   = "leeto";
  • 从位置 0 开始：haystack[0…4] = “leetc”，不等于 needle。
  • 继续滑动窗口直到末尾，也没匹配 → 返回 -1。

✅ 总结：

  • indexOf 内部帮你实现了 子串搜索算法（暴力 / Boyer-Moore / 优化）。
  • 你一行调用它，就等价于把整个查找逻辑搬过来了。
  • 所以这道题其实考的不是写 indexOf，而是 能否自己实现一个类似功能，比如用暴力或 KMP。

下面给你一个KMP（Knuth–Morris–Pratt）版本的 strStr 实现（Java），以及要点讲解。

思路速览

  • 目标：在主串 haystack 中找模式串 needle 的第一次出现位置。
  • 关键：预处理 needle 得到 最长相等前后缀表（也叫 lps 或 next 数组），当失配时，模式串可以按照 lps 跳过一部分，避免主串回退，整体时间复杂度 O(n + m)。

代码（Java）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution {
    public int strStr(String haystack, String needle) {
        if (needle.length() == 0) return 0;      // 习题定义：空模式返回 0
        if (haystack.length() < needle.length()) return -1;

        char[] s = haystack.toCharArray();
        char[] p = needle.toCharArray();

        int[] lps = buildLps(p); // 构建模式串的最长前后缀数组

        int i = 0; // haystack 指针
        int j = 0; // needle   指针
        while (i < s.length) {
            if (s[i] == p[j]) {
                i++;
                j++;
                if (j == p.length) {
                    return i - j;   // 找到第一次出现的位置
                }
            } else {
                if (j > 0) {
                    j = lps[j - 1]; // 利用 lps 回退 needle 的指针
                } else {
                    i++;            // j==0，无可回退，只能推进主串
                }
            }
        }
        return -1;
    }

    // 构建 lps（Longest Prefix that is also Suffix）数组
    // lps[k] 表示 p[0..k] 这个前缀的“最长真前缀==后缀”的长度
    private int[] buildLps(char[] p) {
        int n = p.length;
        int[] lps = new int[n];
        // len 表示当前前后缀的匹配长度，lps[0] = 0
        int len = 0;
        for (int i = 1; i < n; i++) {
            while (len > 0 && p[i] != p[len]) {
                len = lps[len - 1];  // 继续回退，寻找更短的可匹配前后缀
            }
            if (p[i] == p[len]) {
                len++;
            }
            lps[i] = len;
        }
        return lps;
    }
}

关键点解释

  1. lps 数组含义

    1
    lps[i]

    ：表示

    1
    needle[0..i]

    这个子串的最长“真前缀 == 真后缀”的长度。

    • 例如模式串 "ababaca" 的 lps 为 [0,0,1,2,3,0,1]。

  2. 匹配过程

    • 若 s[i] == p[j]：两指针同时右移。若 j 达到 p.length，说明完全匹配，返回起始下标 i - j。
    • 若不匹配：
      • 若 j > 0，利用 lps[j-1] 回退 j，避免回退 i；
      • 若 j == 0，只能推进 i。

  3. 复杂度

    • 构建 lps：O(m)
    • 匹配过程：O(n)
    • 总计：O(n + m)，空间 O(m)。

小例子走一下

  • haystack = "sadbutsad"

    1
    2
    3

    , 

    
needle = "sad"

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10

      - `needle` 的 `lps = [0,0,0]`
      - 从 i=0, j=0 开始，连续三次匹配成功，j==3 → 返回 `i-j = 0`。

    ------

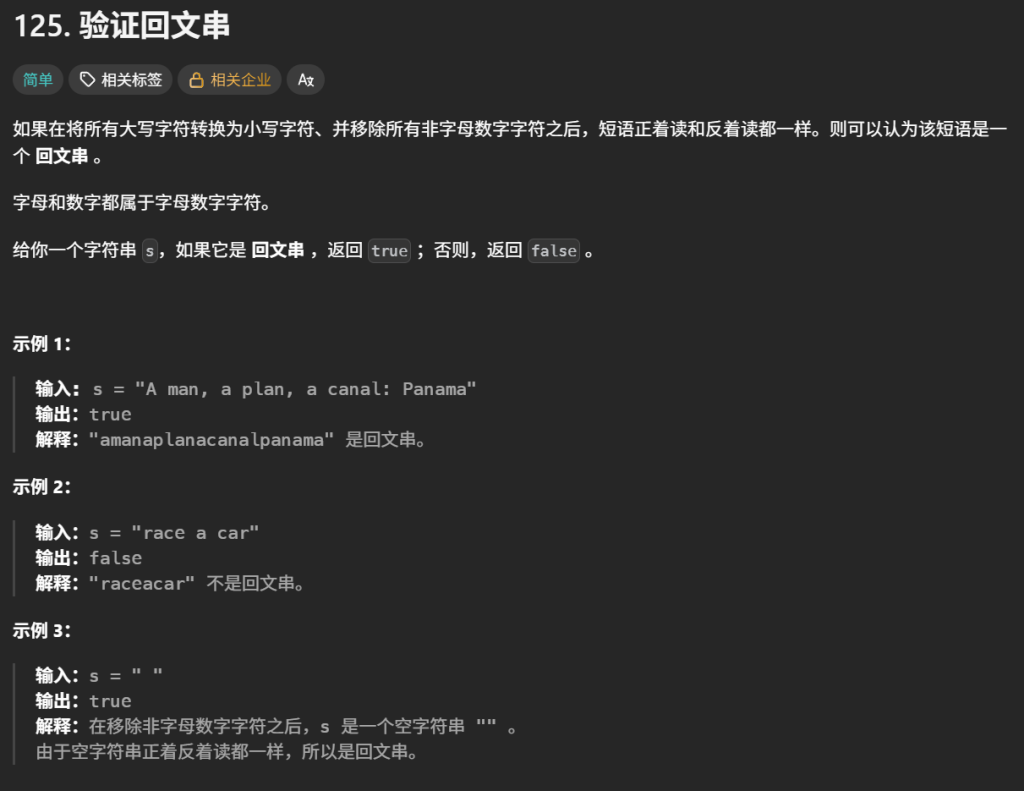
    ## 8.验证回文串（简单）

    ![img](https://www.legendkiller.xyz/wp-content/uploads/2025/09/image-420-1024x791.png)

class Solution {
public boolean isPalindrome(String s) {
// 将字符串转换为小写字母
s = s.toLowerCase();
// 定义两个指针，分别指向字符串的开头和结尾
int left = 0;
int right = s.length() - 1;
while (left < right) {
// 如果左指针指向的字符不是字母或数字，则右移
if (!Character.isLetterOrDigit(s.charAt(left))) {
left++;
} else if (!Character.isLetterOrDigit(s.charAt(right))) {
// 如果右指针指向的字符不是字母或数字，则左移
right–;
} else if (s.charAt(left) != s.charAt(right)) {
// 如果左右指针指向的字符不相等，则返回false
return false;
} else {
// 否则，同时左移和右移
left++;
right–;
}
}
// 如果循环结束都没有返回false，则说明字符串是回文串
return true;
}
}

1
2
3

方法2

class Solution1 {
public boolean isPalindrome(String s) {
// 将字符串转换为小写字母
s = s.toLowerCase();
//定义集合存放字符
StringBuilder sb = new StringBuilder();
for (int i = 0; i < s.length(); i++) {
// 如果字符是字母或数字，则添加到集合中
if (Character.isLetterOrDigit(s.charAt(i))) {
sb.append(s.charAt(i));
}
}
// 正序遍历和倒序遍历，比较字符是否相同
for (int i = 0; i < sb.length(); i++) {
if (sb.charAt(i) != sb.charAt(sb.length() - 1 - i)) {
return false;
}
}
return true;
}
}

1
2
3
4
5
6
7
8
9

## 9.判断子序列（简单）

![img](https://www.legendkiller.xyz/wp-content/uploads/2025/09/image-421-1024x617.png)

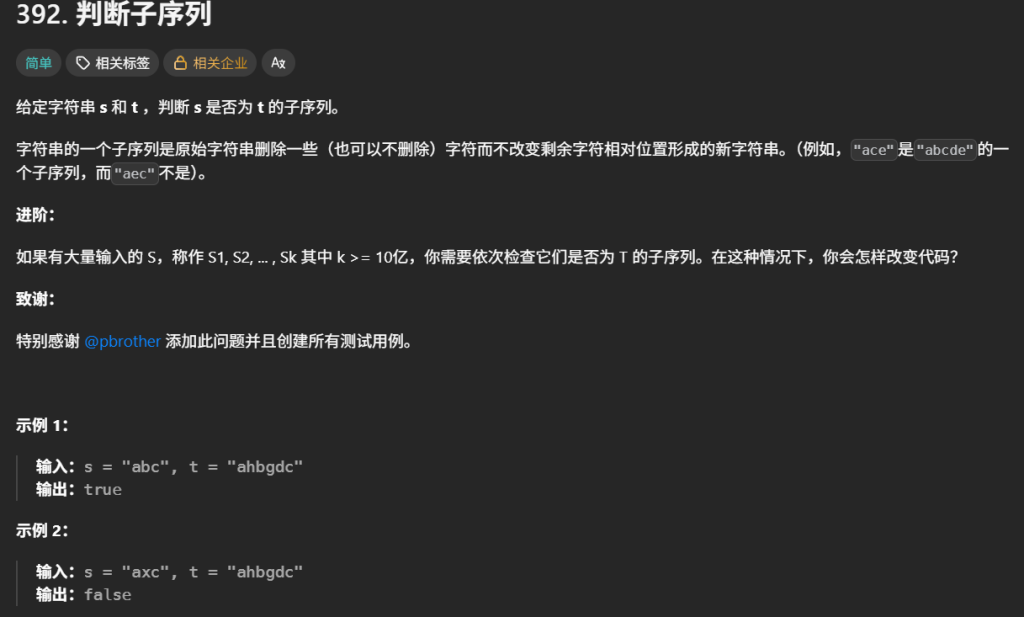
双指针法

左指针指向s字符串，右指针指向t字符串

class Solution {
public boolean isSubsequence(String s, String t) {
int left = 0; // 指针1，遍历 s
int right = 0; // 指针2，遍历 t

    while (left < s.length() && right < t.length()) {
        if (s.charAt(left) == t.charAt(right)) {
            // 当前字符匹配成功，移动 s 的指针
            left++;
        }
        // 不管是否匹配，t 的指针都要往前走
        right++;
    }
    // 如果 s 的所有字符都被匹配完，则说明 s 是 t 的子序列
    return left == s.length();
}

}

1
2
3
4
5

## 10.赎金信（简单）

![img](https://www.legendkiller.xyz/wp-content/uploads/2025/09/image-422-1024x794.png)

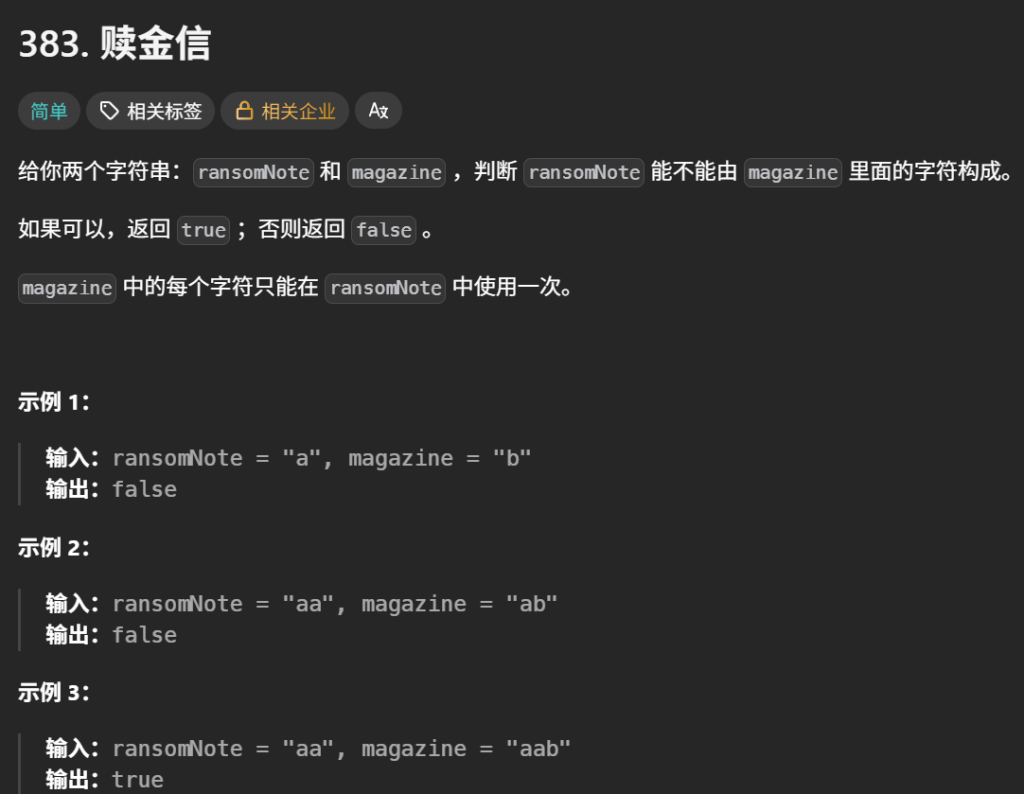class Solution {
public boolean canConstruct(String ransomNote, String magazine) {
if (ransomNote.length() > magazine.length()) {
return false;
}
int[] count = new int[26];
//统计每个magazine字符出现的次数
for (char c : magazine.toCharArray()) {
count[c - ‘a’]++;
}
//遍历ransomNote，如果字符在magazine中出现过则计数减一
for (char c : ransomNote.toCharArray()) {
if (count[c - ‘a’] == 0) {
return false;//如果字符在magazine中未出现过，则返回false;
}
//如果字符在magazine中出现过，则计数减一
count[c - ‘a’]–;
}
return true;
}
}

1
2
3
4
5

## 11.同构字符串（简单）

![img](https://www.legendkiller.xyz/wp-content/uploads/2025/09/image-423-1024x765.png)

class Solution {
public boolean isIsomorphic(String s, String t) {
if (s.length() != t.length()) {
return false;
}
int[] sMap = new int[256];//记录s中每个字符出现的次数
int[] tMap = new int[256];//记录t中每个字符出现的次数
// 遍历字符串s和t，如果两个字符在各自映射表中出现的次数不同，则返回false;
for (int i = 0; i < s.length(); i++) {
char sc = s.charAt(i);
char tc = t.charAt(i);

        // 检查s中的字符sc在sMap中的映射值与t中的字符tc在tMap中的映射值是否相等
        if (sMap[sc] != tMap[tc]) {
            return false;
        }
        // 更新sMap和tMap，将当前字符的映射值设置为当前索引i+1
        sMap[sc] = i + 1;
        tMap[tc] = i + 1;
        
    }
    return true;
}

}