文法

G=(VN,VT,P,S)

VN:非终结符（大写） VT：终结符（小写） P：规则集合 S：开始符号

题一

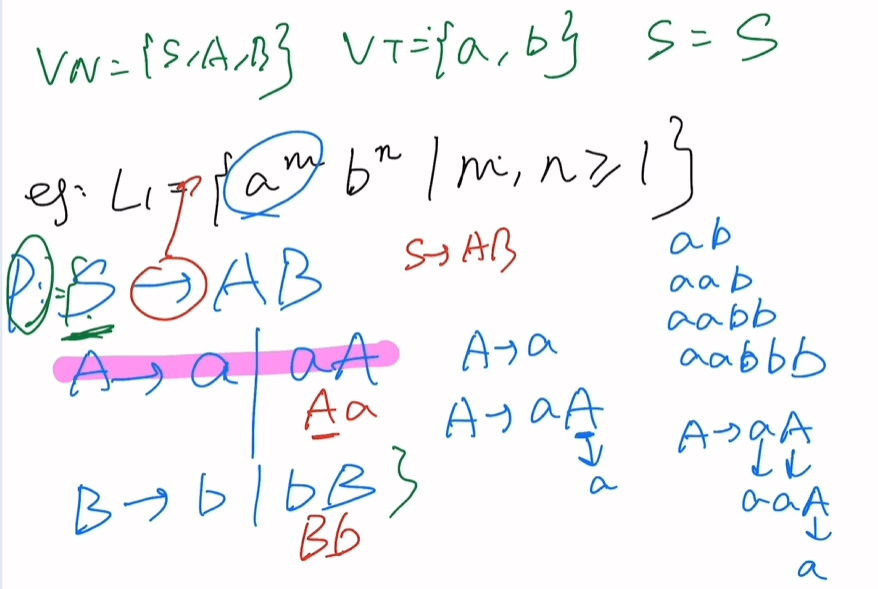
L1={ambn|m,n≥1}

当m=1，n=1 ab m=2，n=1 aab …aabb aabbb

S->AB

A->a|aA

B->b|bB

即VN={S,A,B}, VT={a,b},S=S,

p={S->AB

A->a|aA

B->b|bB}

题二

L2={anbnci|n≥1,i≥0}

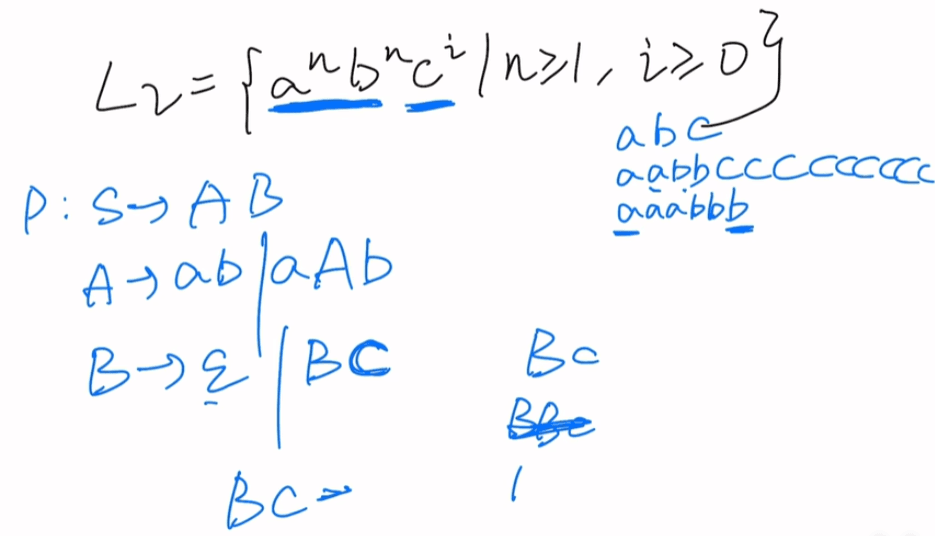
ab,abc,aabbc,aabbcc

S->AB

A->ab|aAb

B->ε|Bc

即VN={S,A,B}, VT={a,b,c},S=S,

p={S->AB

A->ab|aAb

B->ε|Bc}

题三

题四

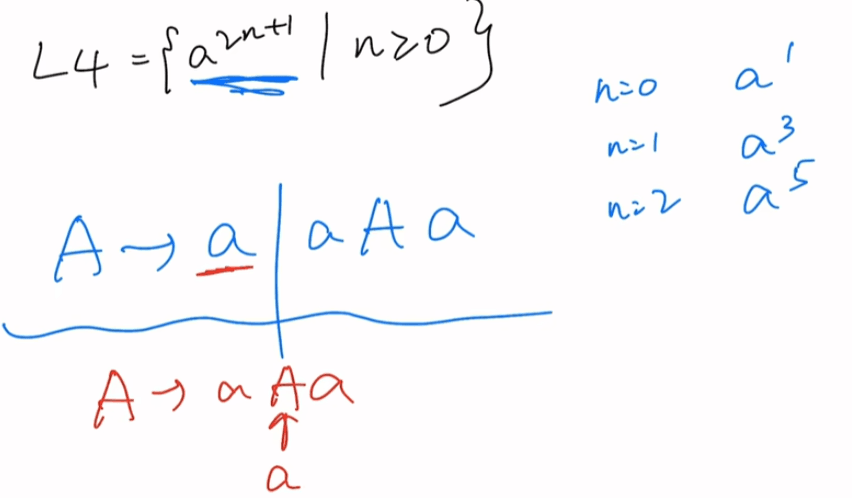
题五

最左推导和最右推导

题一

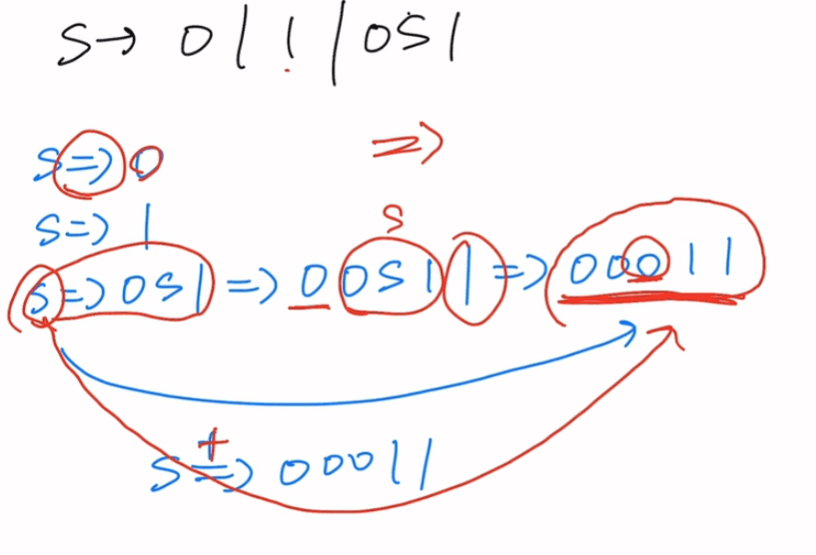
推导箭头带加号，意为广义推导，表示跳过了好几步直接得到最终结果

最左推导：以左边为基准

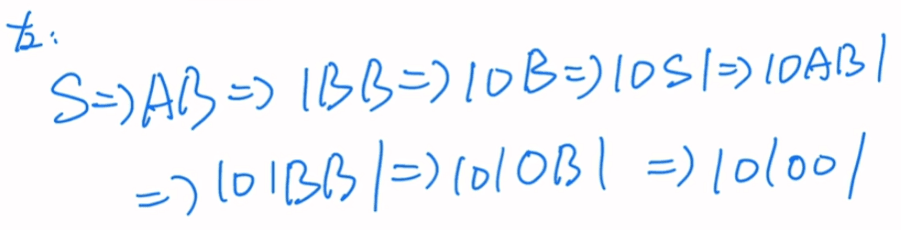
最右推导：以右边为基准

AAB1=> AA01=> A1B01 =>A1001

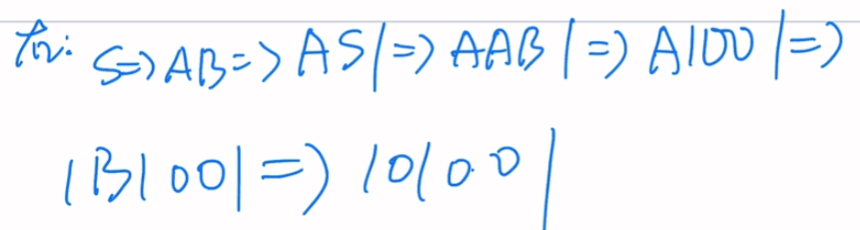
题二

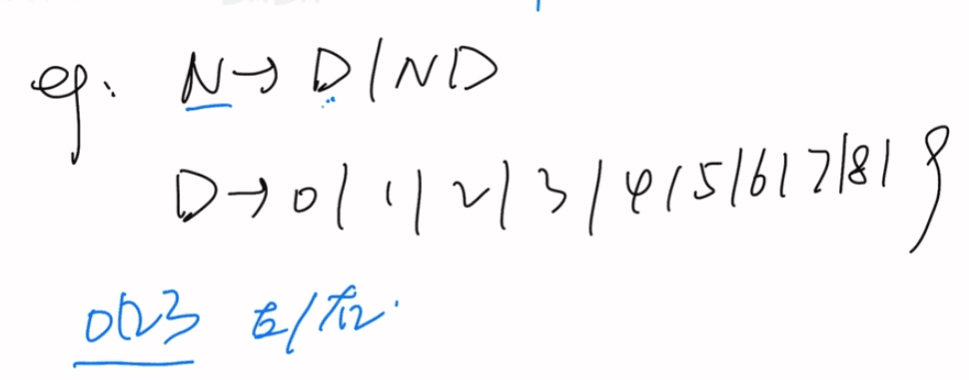
最左推导

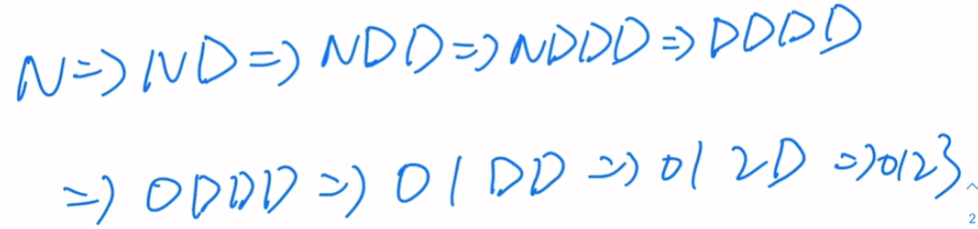
最右推导

N=>ND=>N3=>ND3=>N23=>ND23=>N123=>D123=0123

归约和语法树

文法的二义性与分类

先进行最左最右推导

左推导树与右推导树

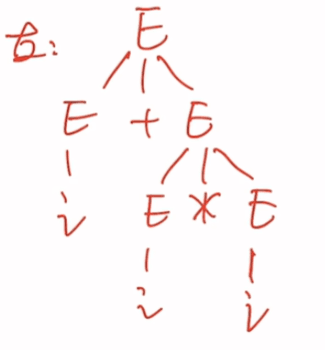
可以发现左右推导树不一样，即二义性

文法分类

0型（无限制文法）

1型（上下文有关）

2型（上下文无关）

3型（正规文法）

0型：

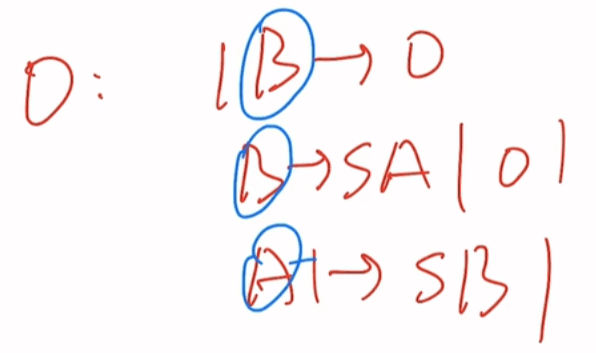
左边至少有一个大写字母（非终结符）

1型：

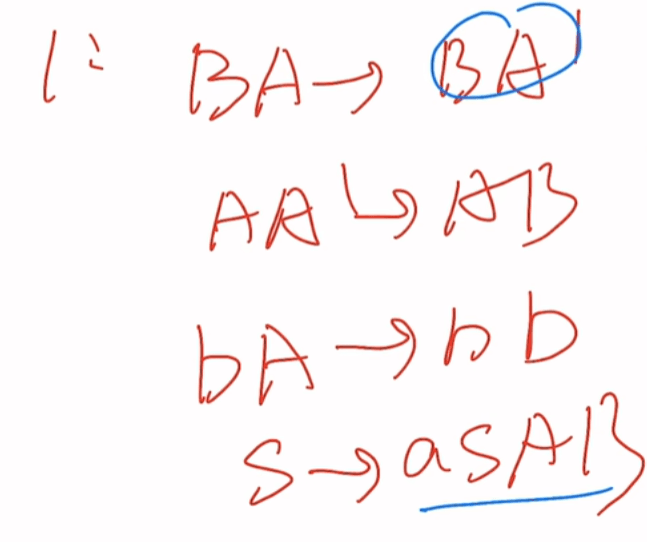
右边长度≥左边长度

2型：

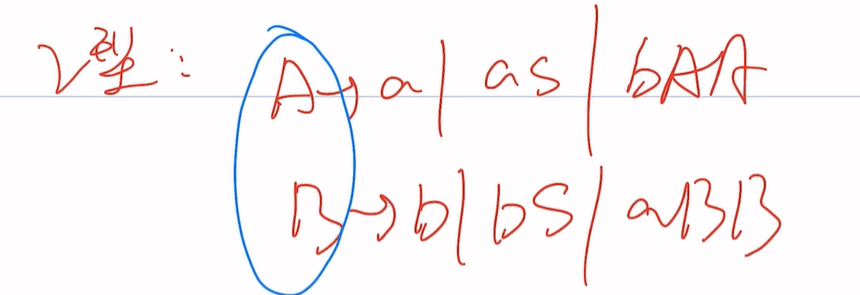
左边只能有一个大写字母（非终结符）

3型：左/右线性文法大概是这个意思：若文法的右边（箭头的右边）有非终结符（大写字母），则这些大写字母必须在所在组合的最左/右边。

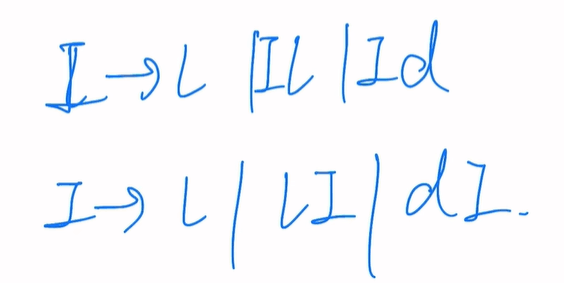
第一行左线性文法

第二行右线性文法

短语直接短语句柄

短语：有子结点的围圈，最边缘

直接短语：一个子结点，围圈高度为2(在短语围的圈里找高度为2的圈)

句柄：最左直接短语

题一

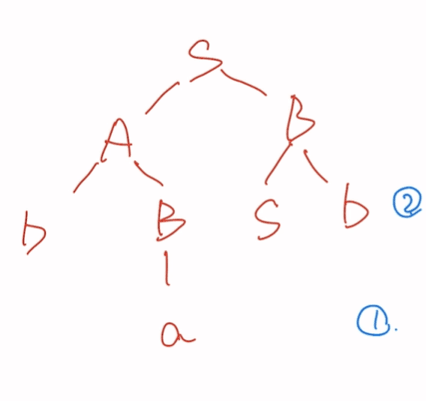
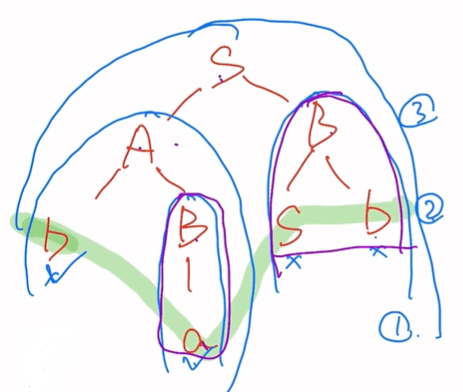
短语：a,ba,sb,basb

直接短语：a,sb

句柄：a

题二

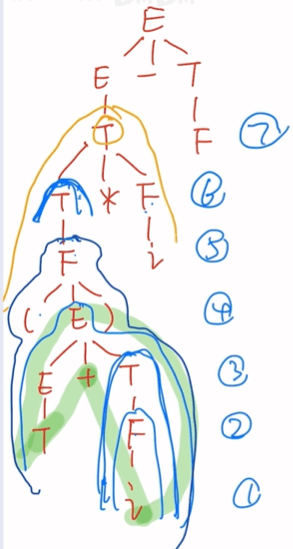
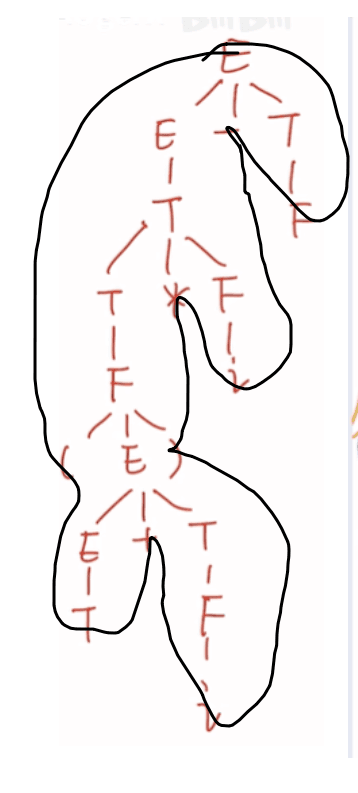
短语：i,T,T+i,(T+i),(T+i)*i,(T+i)*i-F

直接短语：i,F,T

句柄：T

正规式到NFA

什么是正规式？

假设要以b开头，要aa结尾的句子发现有很多情况比如，baa，bbaa,bxxxxaa（xxxx又能取ab的各种组合）

用正规式表达就是（a|b）*

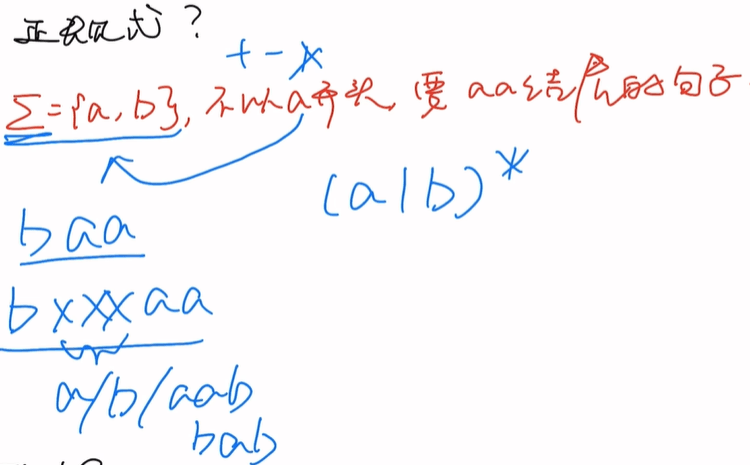
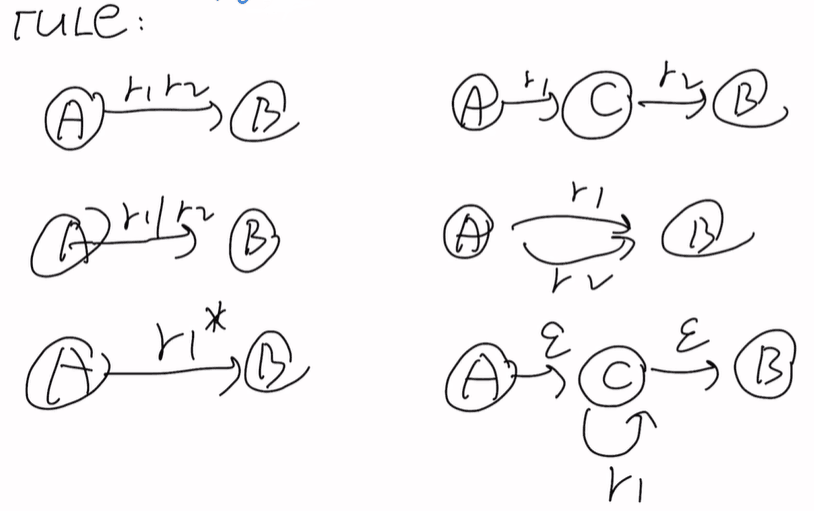
rule规则

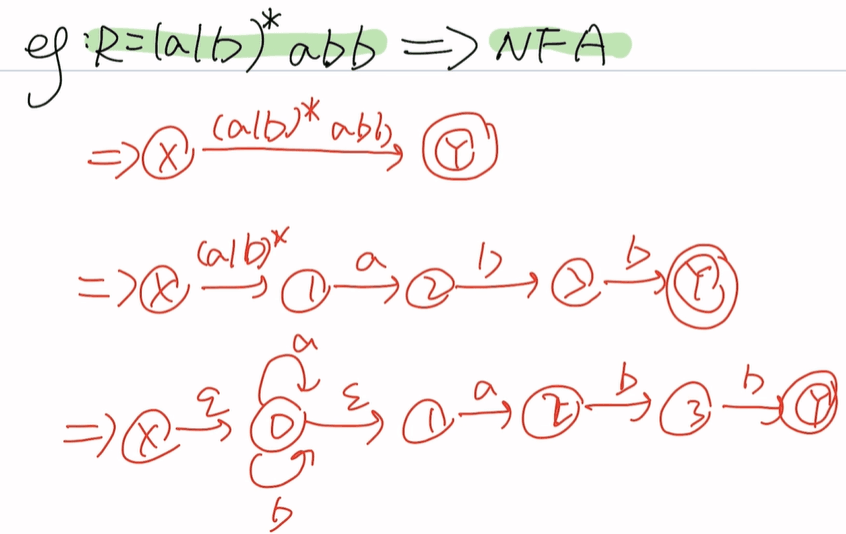
题一

（a|b）*为一组abb为一组开始符号一个圈，末态两个圈

题二

l一组，(l|d)*一组

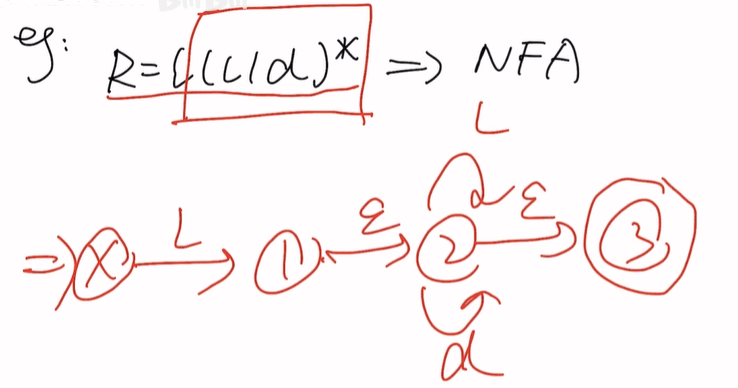
NFA到DFA（子集法）

NFA怎么转到DFA：子集法

也就是列一个表

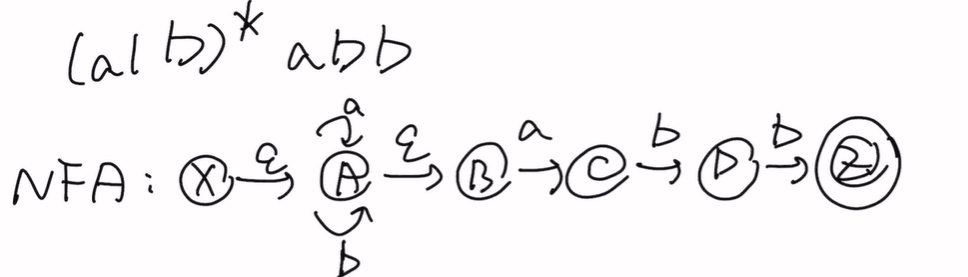
空串可以看做氮气加速，不耗体力前往下一项

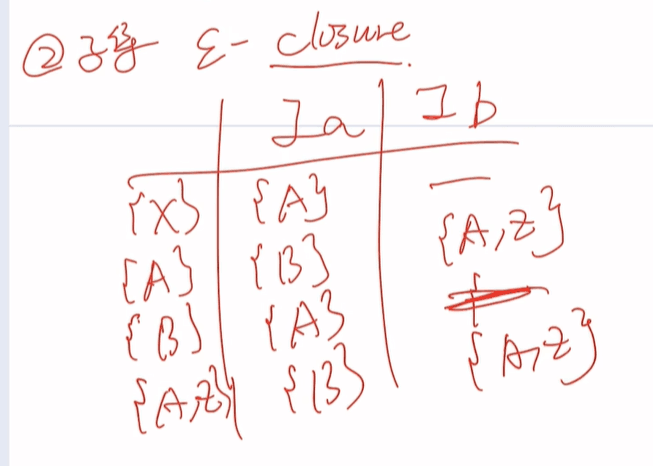
初始状态为什么是{X,A,B}：因为X后有空串可以氮气加速到A或者B

{ABC}怎么来的？当给初始状态一个a，对于X：它本身就可以通过氮气到A，又根据第二次氮气到B，之后给a直接到C。对于A：同理先氮气到B，给a直接到C。对应B：给a直接到C

第二个{ABC}怎么来的？当给一个a，对于A:给它一个a本身就能到A，后通过氮气到B。对于B：给a到C。对于C：没有效果

后面的填表跟前面一样，不再阐述

	Ia	Ib
初始状态{X,A,B}	{A,B,C}	{A,B}
写未探索的{A,B,C}	{A,B,C}	{A,B,D}
写未探索的{A,B}	{A,B,C}	{A,B}
写未探索的{A,B,D}	{A,B,C}	{A,B,Z}
写未探索的{A,B,Z}	{A,B,C}	{A,B}

由于我们末态是Z,在表中先标出Z的位置，我们给表设置数字，看看右边的数据对应左边的几号如图

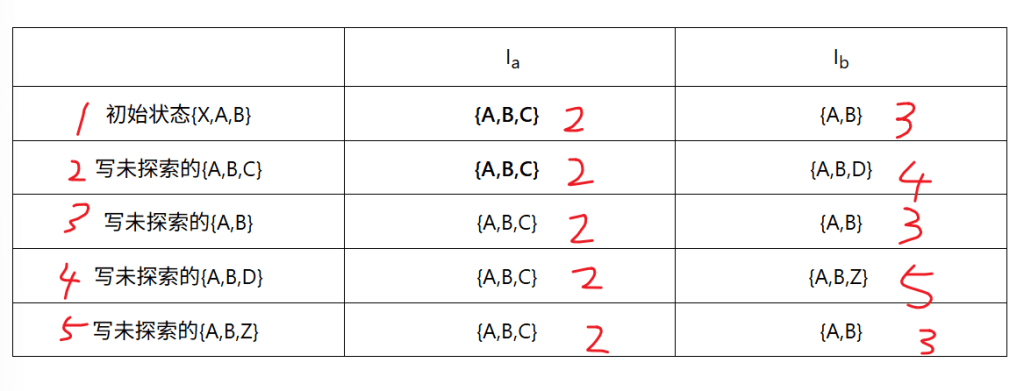
简化一下：

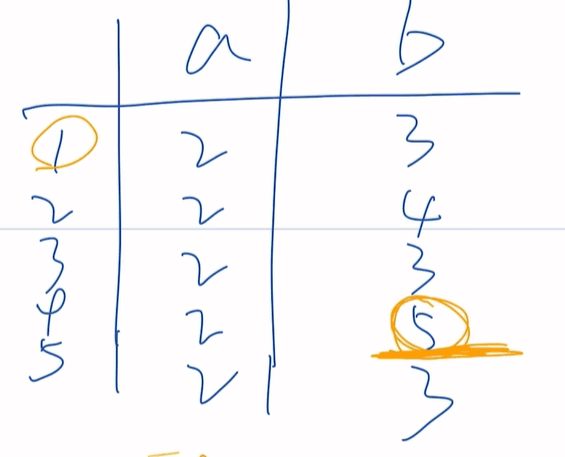
最小化DFA(找IKUN)

分状态，先大分，5末态单独分一组（5末态默认为IKUN）

即{1,2,3,4}{5}

{1,2,3,4}a={2}

{1,2,3,4}b={3,4,5}出现了5,抓住4这个ikun了

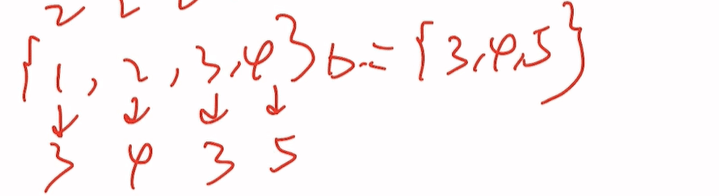
抓到ikun后更新一轮分组

即{1,2,3}{4}{5}

{1,2,3}a={2}

{1,2,3}b={3,4}出现了4，抓住2这个ikun

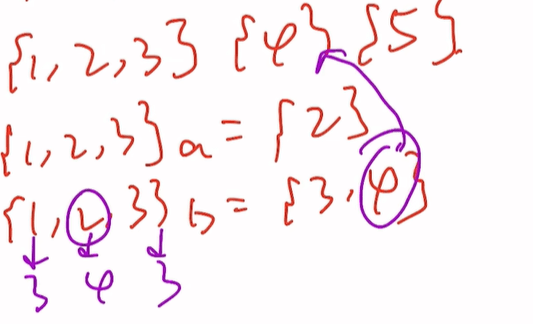
抓到ikun后更新一轮分组

{1,3}{2}{4}{5}

{1,3}a={2}出现了2,{1,3}都是ikun那就不用分了

即最终的状态是：{1,3}{2}{4}{5}

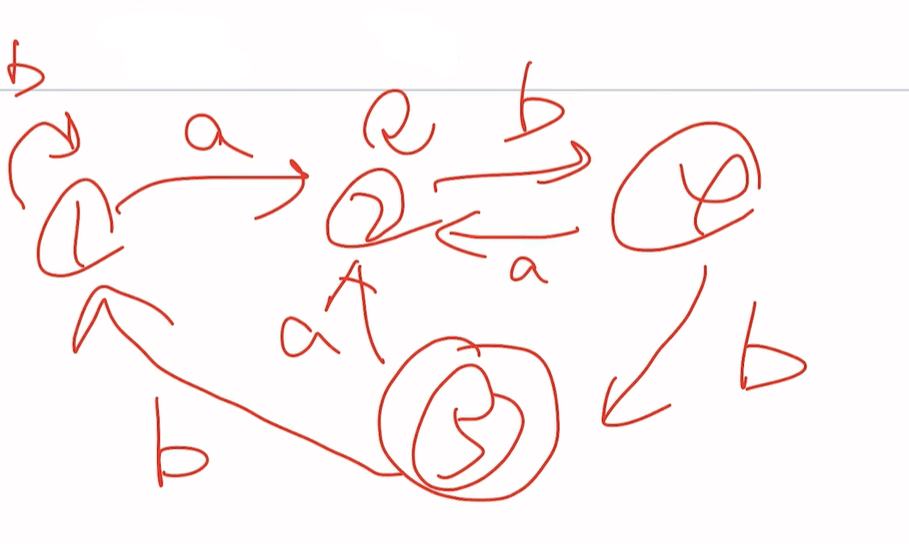
1，3共体只用画一个

这里面12345也可以换成ABCDE都是一样的

正规文法到DFA

首先要了解正规文法->正规式

1为右线性文法 2为左线性文法

题一

注意两个要点 -> 变为 = | 变为 + 即下图

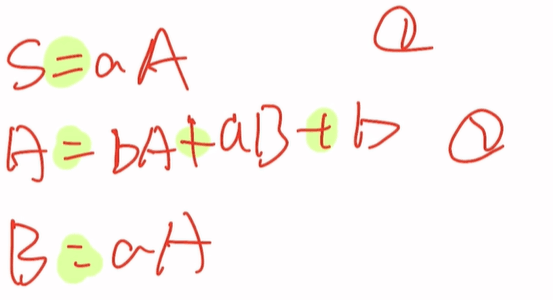
最后要求出正规式即S=( )的形式

带入方程得S=a（b+aa）A+b，发现符合这一条规则

即S=a(b+aa)*b=a(b|aa)*b

正规文法->正规式->NFA->子集法->DFA->最小化DFA

接下来就是正规文法到DFA的过程：我们已经得到了正规式接下先得到NFA再通过子集法得到DFA最后再通过最小化DFA得到最后的结果

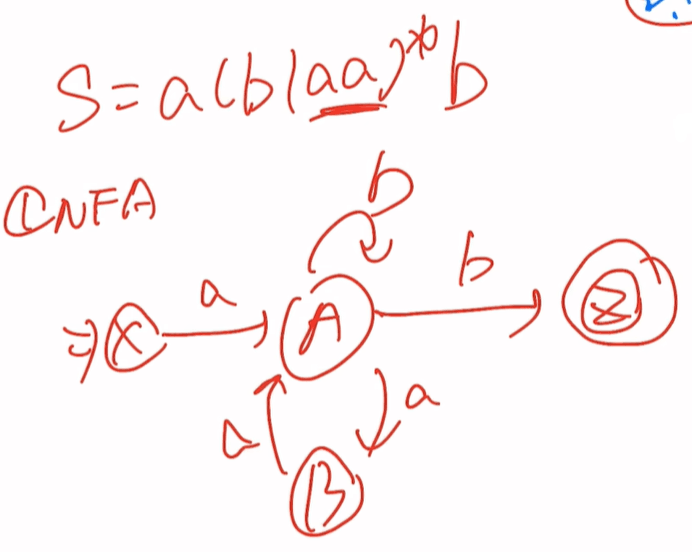
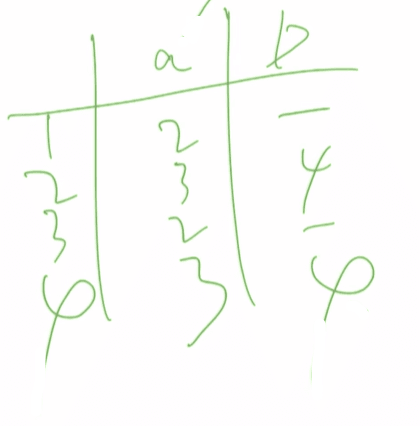
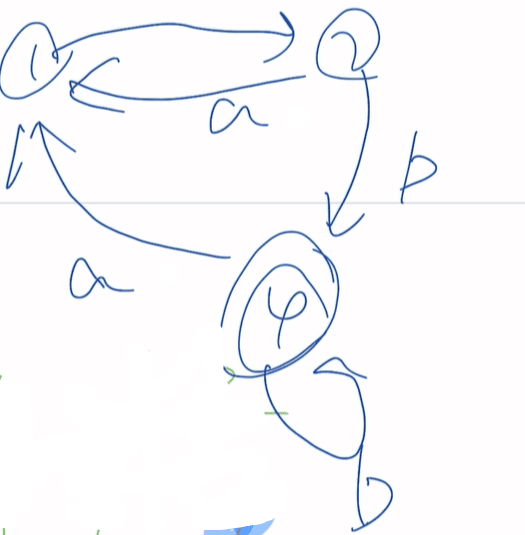
最小化DFA{1,2,3}{4}找小黑子过程略

结果{1,3}{2}{4}

消除左递归

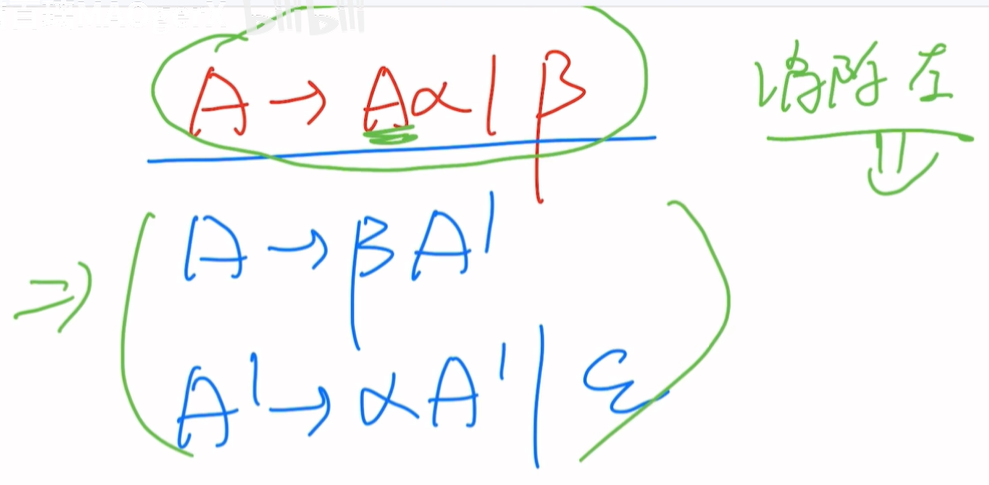
2条规则如上图

题一

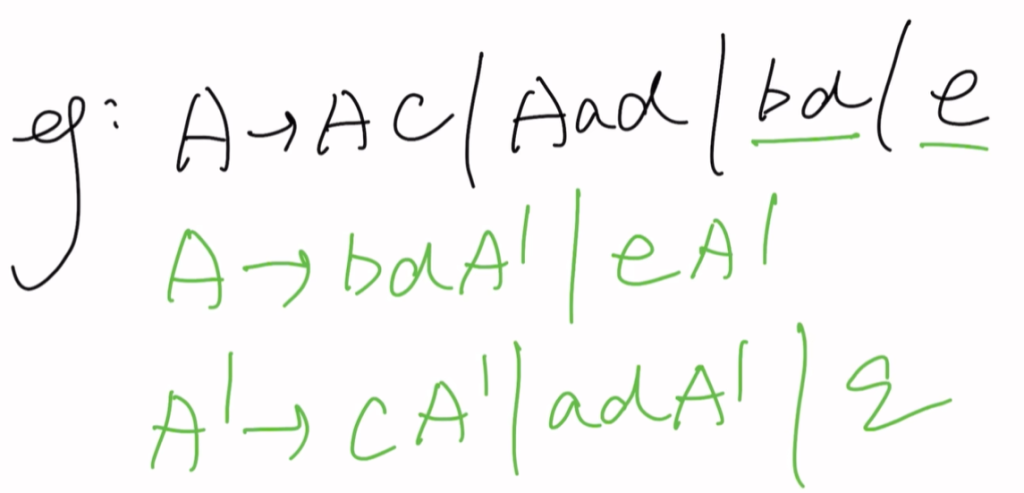
题二

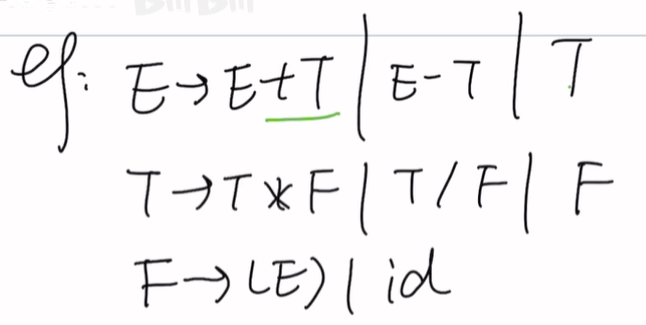
First集与Follow集

First集：看产生式左边第一个小写字母（终结符）eg:l,i,* …

Follow集：看右边

（1）开始符号集合加#

（2）A->αB 则Follow（B）=Follow(A) （B右边没有卫兵）

（3）A->αBβ(B后不为空)

β小写，直接写
β大写，Follow（B）= First（β）- ε

当：β-> ε,再来规则（2）

题一

First集：

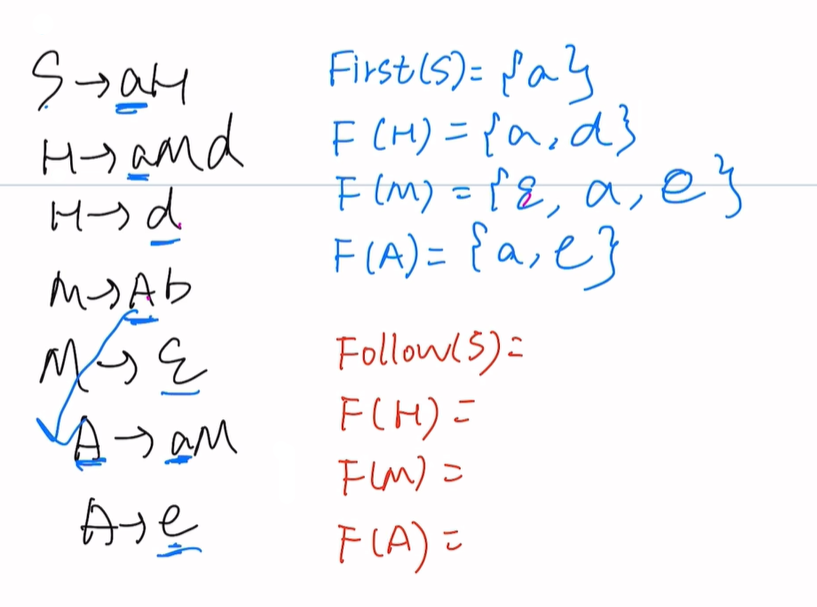
Follow集：

例如Follow（S）：在右边找S，直接为空，但是S是开始符号所以要加#

注：第一个Follow就是开始符号，必须加#

Follow（H）：在右边找H,即S->aH，H没有卫兵找规则（2）即Follow（H）=Follow（S）=#

Follow（M）：在右边找M，有两个第一个中M右边卫兵是d为小写直接写，第二个M右边没卫兵Follow（M）=Follow（A），Follow（A）目前不知道，等我们算出来再补上去

接下来同理，过程略

题二

First集：

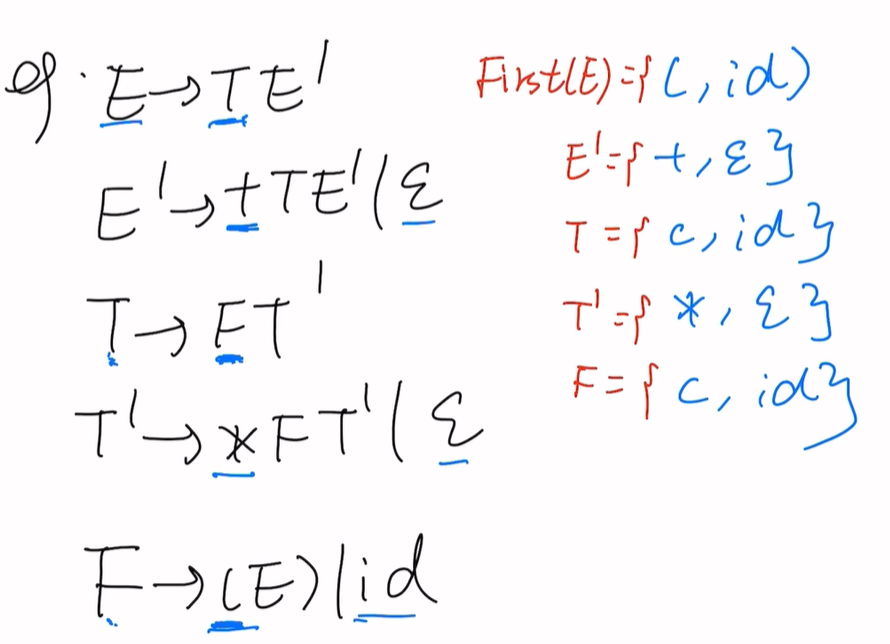
Follow集：

Follow（T）:两种情况

第一种：T后边是E’（有卫兵且大写）按照规则Follow（T）=First（E’）-ε

即{+，ε}-ε = {+}

第二种：E’能推出空串ε，再来一次规则（2），即Follow（T）=Follow（E’）=